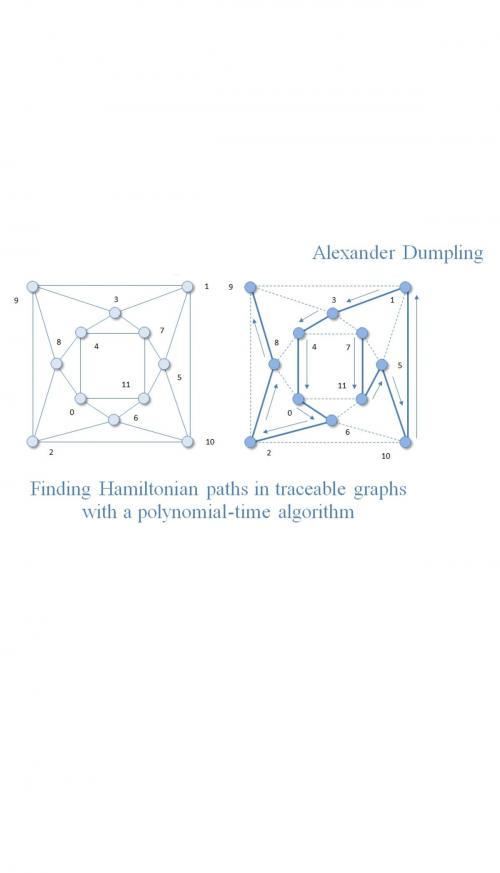
Finding Hamiltonian paths in traceable graphs with a polynomial-time algorithm
Nonfiction, Computers, Programming| Author: | Alexander Dumpling | ISBN: | 6610000075652 |
| Publisher: | PublishDrive | Publication: | June 1, 2018 |
| Imprint: | PublishDrive | Language: | English |
| Author: | Alexander Dumpling |
| ISBN: | 6610000075652 |
| Publisher: | PublishDrive |
| Publication: | June 1, 2018 |
| Imprint: | PublishDrive |
| Language: | English |
Among different classes of computational complexity, NP-complete problems are those of particular practical significance. The class of NP-complete problems considers those problems that are more difficult than other problems in NP and which are currently considered to be unlikely to be solvable (that is, they're unlikely to be decision problems from P). The question that is currently not answered is whether the class of decision problems that can be solved in polynomial time with a deterministic Turing machine is equal to the class of NP problems, P = NP.
We consider the Hamiltonian-path problem in undirected finite graphs with no multiple edges between a given pair of nodes as a problem that is known to be NP-complete. Any other decision problem from NP is known to be polynomial-time reducible to the Hamiltonian-path problem, which implies that having found a polynomial-time algorithm to resolve it, we would also be able to resolve any other problem from NP with a polynomial-time algorithm and thus demonstrate that P = NP.
If it could be demonstrated that P = NP, there would be polynomial-time algorithms for computational problems that are currently considered unsolvable but currently the overwhelming consensus is that P is not equal to NP. Unless P = NP, there are problems in NP that are neither in P nor NP-complete. A polynomial-time algorithm for a problem known to be NP-complete would be a stunning breakthrough.
The Hamiltonian-Path algorithm described in the current work has been developed by Alexander Dumpling. You will be allowed to apply the results from this work and the algorithm in your practical computational situations, provided that you confirm and acknowledge the authorship of Alexander Dumpling with regard to the algorithm described in the current work.
Among different classes of computational complexity, NP-complete problems are those of particular practical significance. The class of NP-complete problems considers those problems that are more difficult than other problems in NP and which are currently considered to be unlikely to be solvable (that is, they're unlikely to be decision problems from P). The question that is currently not answered is whether the class of decision problems that can be solved in polynomial time with a deterministic Turing machine is equal to the class of NP problems, P = NP.
We consider the Hamiltonian-path problem in undirected finite graphs with no multiple edges between a given pair of nodes as a problem that is known to be NP-complete. Any other decision problem from NP is known to be polynomial-time reducible to the Hamiltonian-path problem, which implies that having found a polynomial-time algorithm to resolve it, we would also be able to resolve any other problem from NP with a polynomial-time algorithm and thus demonstrate that P = NP.
If it could be demonstrated that P = NP, there would be polynomial-time algorithms for computational problems that are currently considered unsolvable but currently the overwhelming consensus is that P is not equal to NP. Unless P = NP, there are problems in NP that are neither in P nor NP-complete. A polynomial-time algorithm for a problem known to be NP-complete would be a stunning breakthrough.
The Hamiltonian-Path algorithm described in the current work has been developed by Alexander Dumpling. You will be allowed to apply the results from this work and the algorithm in your practical computational situations, provided that you confirm and acknowledge the authorship of Alexander Dumpling with regard to the algorithm described in the current work.